The computer automatically scores all plays and adds them to a player's total score.

The board is made up of regular and special squares. 

Special squares may increase or decrease the score for a play. DOUBLE- and TRIPLE-THE-LETTER squares increase the value of a letter played on them. DOUBLE- and TRIPLE-THE-WORD squares increase the value of a word played on them.

Twenty Squares allow the player to flip the tile and use it as though it were an asterisk -- reducing the tile played to zero point value but allowing that tile to represent any letter or string of letters.

Finally, four special squares subtract from the value of a play as a whole.

The first play must cover the centermost square..

The program's scoring procedure is as follows:

1. Find all new words made
2. Figure the value of each new word made
3. Add those values
4. Make special adjustments for the play as a whole
 

For example:

The first player plays:

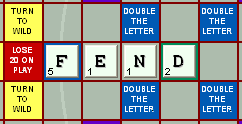
Only one word is played here -- FEND.  It's not possible to make more than one word on the first play since all plays must be a string of tiles laid down in either a horizontal or a vertical direction leaving no gaps between the first and last tile of the play. The first play is also the game's only play that need not attach to tiles already on the board.

The "F" is played on a DOUBLE-THE-LETTER square. Thus the initial score for the word is 2X5 (F) + 1(E)+ 1(N) + 2(D), which totals 14.

The "D" covers the centermost square which is a DOUBLE-THE_WORD square.

Thus the value for the play is 2X14, which totals 28.

The second player plays:

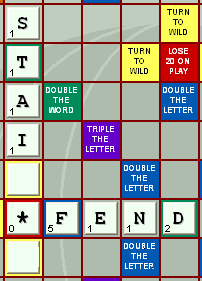
This player has made two words, DEFEND and STAINING.

DEFEND is worth 0 + 5 + 1 + 1 + 2, which totals 9 points. Since the FEND tiles were previously played, the second player is neither benefited nor penalized by special squares under FEND's letters.

To make STAINING the player took advantage of 2 squares that allow and force him to flip the tile and use it as though it were an asterisk -- thus also losing the point value for  those letters. The orgininal letters do not show on the screen.

The points for the word are 1 + 1 + 1 + 1 + 0 + 0 + 0, which totals 4.

Since the player placed the "A" on a DOUBLE-THE-WORD square, the value of the word is 2 * 4, which is 8.

Thus the combined value for the two words the player made is 9 + 8, which totals 17.

However, the player also covered a LOSE-20-ON-PLAY square, which brings the total score to 17 - 20, or minus 3.

Of course, the player did this because it allowed him to collect the 40 bonus points for using all seven tiles in the same play.

The score for the play is thus -3 + 40, which totals 37.

The first player now plays:

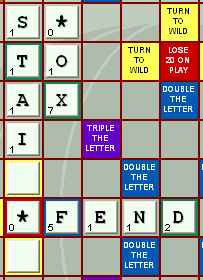
This player has made 4 new words -- SO, TO, AX, and FOX.

SO is worth 1 points.

TO is worth 2 points. (The T was already played, so the Double The Word square under it does not count.)

AX is worth 8 points, but the X was placed on a DOUBLE-THE-WORD square, which makes that word 16 points.

FOX is worth 8 points, but again the X is on a DOUBLE-THE-WORD square, which makes that word 16 points.

The total score for the play is the total of all the new words made, 1 + 2 + 16 + 16, which totals 35 points.

There are no adjustments to this total since the player neither covered a LOSE-20-ON-PLAY square nor used seven tiles in the play.

Of course when an asterisk is involved in a play you may never know exactly what word your opponent is actually making unless you challenge.